How To Calculate The Mean Average Of For Grouped Data From A Frequency Distribution Table
In this video we discuss how to calculate the mean or average for grouped data, such as from a frequency distribution table. We go through this process step by step, from finding the class midpoints to summing the midpoints times the frequencies.
Transcript/notes
Mean for grouped data
In this video we are going to discuss how to find the mean for grouped data, such as the data in a frequency distribution table.
In a past video we discussed what a frequency distribution is. Real quick, you have a data set, you break the data down into classes or intervals, column 1, you tally up how many data points are in each class, column 2, and you write that number down, which is the frequency, column 3.
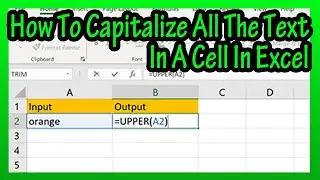
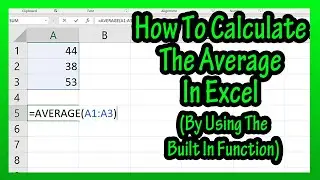
So let’s find the mean for the grouped data shown on the screen. The first thing that we need to do is find the midpoints of each of the classes, and the formula for finding the midpoint of a class is the lower class limit plus the upper class limit and divide that by 2. So, for class one, the lower limit is 126, add that to the upper limit of 174 to get 300 and divide that by 2 and we get 150 as the midpoint for class 1.
Continuing this process for the remaining 6 classes we get, 199, 248, 297, 346, 395, and 444.
To make things clearer, we are going to label frequency as f, and class midpoint as xm, where m can be 1 to 7, the number of classes we have.
The next thing that we are going to do is multiply the frequencies for each class times the midpoints for each class and we will create a new column in our table for that.
So, for class 1 we have a frequency of 5 and multiply that by the midpoint of 150 and we get 750. For class 2 we have a frequency of 5 and a midpoint of 199, which gives us 995. And we will continue this for the 5 remaining classes as you see in the table.
Next we are going to find the sum of the last column, the frequency times the midpoint column, and adding these up we get 21442. And we also want to find the sum of the frequencies, which is 75.
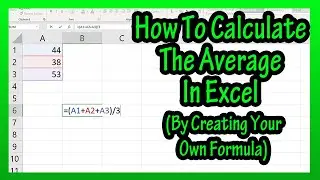
Now that we have the sum of these numbers, we can find the mean of our grouped data, and to do this we are going to take the sum of the last column, the frequency times the midpoint column, and divide it by the sum of the frequencies. So, 21442 divided by 75 equals 285.893, rounding off we get 285.9.
The formula that is often used for this process is usually written as x bar equals sum of the midpoints of the classes times the frequencies of the classes divided by the total number of frequencies.
This symbol is the Greek letter sigma and in mathematics, it means sum of, and the x bar represents the mean.
Basically in this process, we have taken the average of each of the classes and multiplied it times the number of data points in each of the classes, added all of those up and divided those by the total number of data points in the data set. This is not going to give us the exact true mean of the data, but it gives us an acceptable approximation of the mean.
Timestamps
0:00 Grouped Data Overview
0:21 Find Midpoints For Each Class
1:01 Multiply Frequencies Times Midpoints
1:40 Calculate The Mean For Grouped Data
