Product Rule Of, For Exponents Explained - How To Multiply Terms With Exponents
In this video we discuss the product rule for exponents and show how the rule works. We also go through examples with more than one term and with different base values.
Transcript/notes
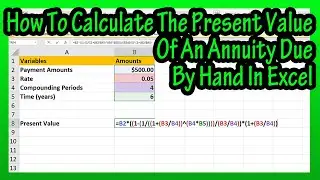
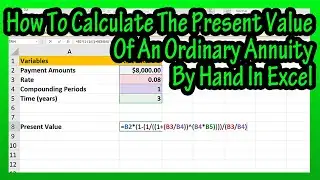
The product rule for exponents only applies to exponents that have the same base value, and it states that a raised to the m times a raised to the n equals a raised to the m plus n.
So, we just add the exponents together. For instance, a raised to the 3 times a raised to the 4. Using the product rule, we just add the exponents together to get a raised to the 7 as the final answer. If we write this out, we have a times a, times a for a raised to the 3, times a times a, times a, times a, for a raised to the 4. So, we have a times itself 7 times, which is a raised to the 7, same answer as before.
And this rule only applies to exponents that have the same base value. For instance, 2 raised to the 3 and 5 raised to the 3 have different base values, so you could not apply the rule.
And this applies for more than 2 terms, such as x raised to the 4 times x raised to the 7 times x. And remember, any term not raised to a power, such as this lone x here has a power of 1. So we have x raised to the 4 plus 7 plus 1, which equals x raised to the 12.
One more example, if we had x raised to the 4 times y raised to the 5 times x raised to the 7 times y raised to the 3, we can still apply the rule to the exponents with the same base values. So we would have x raised to the 4 plus 7 times y raised to the 5 plus 3, which gives us an answer of x raised to the 11 times y raised to the 8.
Timestamps
0:00 Product rule for exponents explained
0:14 Example problem
0:41 For more than 2 terms
1:00 For more than 1 variable