Types Of Errors And Levels Of Significance In Hypothesis Testing - Type One And Type Two Errors
In this video we go through a basic overview of the types of errors and levels of significance in hypothesis testing. We discuss what is a type one and type two error, and how the level of significance decreases the probability of making a type one error in hypothesis testing.
Transcript/notes
When we do hypothesis tests, we always assume the null hypothesis is true, regardless of if the null or alternative hypothesis represents the claim. So, we make one of 2 decisions, reject the null hypothesis or fail to reject the null hypothesis. And, in hypothesis testing, the decision to reject or fail to reject the null hypothesis is based on a sample, not the entire population, so, there is always going to be the possibility of making a wrong decision, an error.
There are 2 types of errors in hypothesis testing, a type 1 and a type 2 error. A type 1 error occurs if the null hypothesis is rejected when it is true, and a type 2 error occurs if the null hypothesis is not rejected when it is false.
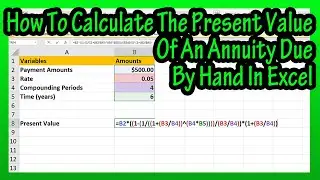
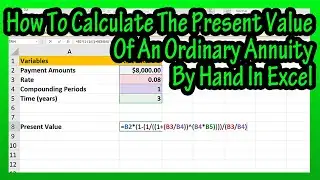
And this box shows the 4 possible outcomes for a hypothesis test.
If h sub 0 is actually true and we do not reject the null hypothesis, a correct decision was made, and if If h sub 0 is actually not true, but we reject the null hypothesis, a type 1 error was made. And if If h sub 0 is actually not true or false, and we do not reject the null hypothesis, a type 2 was made, and if If h sub 0 is actually not true or false, and we reject the null hypothesis, a correct decision was made. A tip is that It may be helpful to remember reject is with type 1 error, and do not reject is with type 2 error.
As an example, let’s say that recent report states that 62% of people get their news from a social media site and you perform a hypothesis test to determine if this is true. When will a type 1 or type 2 error occur?
So, the claim is that the population proportion, p, is equal to 0.62. The null hypothesis contains the equality, so h sub 0 is p = 0.62, and the alternative hypothesis is the complement of the null hypothesis and contains the inequality, so, h sub a is p does not = 0.62.
A type 1 error will occur if you reject the null hypothesis, that p = 0.62, and the actual population proportion does = 0.62.
And a type 2 error will occur if you do not reject the null hypothesis, that p = 0.62, and the actual population proportion does not = 0.62.
Now for the level of significance. There is always a possibility that we reject the null hypothesis, when it is actually true, a type 1 error. But, we can decrease the probability of this happening by lowering the level of significance. And the level of significance is the maximum probability of committing a type 1 error. It is usually noted as the symbol alpha, so, probability of type 1 error = alpha.
The 3 commonly used levels of significance are alpha = 0.10, alpha = 0.05, and alpha = 0.01. And what these figures are saying is when alpha = 0.10, there is a 10% chance of rejecting a true null hypothesis, when alpha = 0.05, there is a 5% chance of rejecting a true null hypothesis, and when alpha = 0.01, there is a 1% chance of rejecting a true null hypothesis.
Timestamps
0:00 Reject Or Fail To Reject The Null Hypothesis
0:23 Types Of Errors In Hypothesis Testing
1:20 Example Problem For Type 1 And Type 2 Errors
2:13 What Is The Level Of Significance In Hypothesis Testing?