Lesson 6: Network Algorithms and Approximations by Mohammad Hajiaghayi: Embedding Tree Applications
In this session, we talk about several applications of probabilistic embedding into trees.
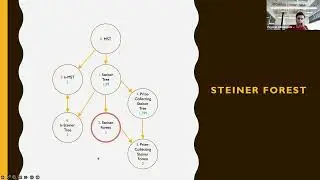
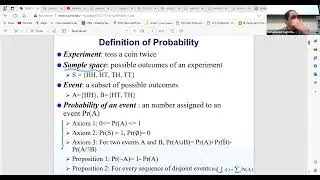
We first focus on the Steiner tree problem, a fundamental network design problem with applications in various fields. The Steiner tree problem involves finding a minimum-cost tree that connects a given set of terminals (vertices) in a graph, potentially including additional vertices called Steiner points. The session discusses the importance of the Steiner tree problem and its relevance to other network design problems.
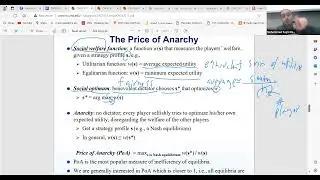
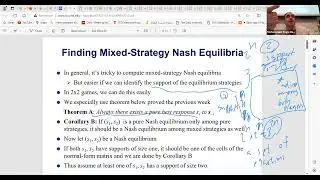
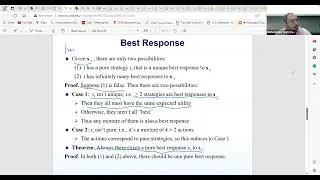
The session also covers the concept of probabilistic embedding into trees, a technique used to simplify network problems by approximating graph metrics with tree metrics. This approach involves embedding the graph into a distribution of trees and solving the problem on each tree, taking the minimum solution as the final result. The session discusses the benefits and limitations of this approach, particularly for the Steiner tree problem.
The session also touches on the concept of useless edges, which can be removed from the graph without affecting the solution, and the importance of considering spanning trees for connectivity problems. It also discusses the use of pre-processing techniques to simplify the graph before applying the probabilistic embedding approach.
Overall, the session provides a comprehensive overview of the Steiner tree problem and its connection to probabilistic embedding into trees. It highlights the challenges and opportunities in solving network design problems using tree embedding techniques.
#steinertree, #networkdesign, #graphembedding, #treeembedding, #probabilisticembedding, #spanningtrees, #approximationalgorithms, #connectivityproblems, #uselessedges, #preprocessing, #optimization, #combinatorialoptimization, #graphalgorithms
![[NRA 2019] NEW Beretta 92X Performance Pistol](https://images.videosashka.com/watch/SpWSjue_8G4)