Lesson 7: Computational Game Theory by Mohammad Hajiaghayi: Analyzing Normal Form Games
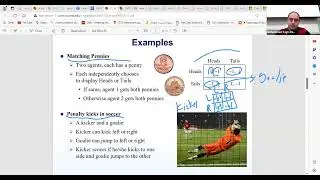
In this session, we started analyzing normal form games. In particular, we revisited the P-Beauty game, where participants choose a number between 0 and 100, aiming to be closest to a fraction (P) of the average number chosen. We experimented with different values of P, and observed how the game's outcomes can reflect social behavior and decision-making patterns. The game illustrates how simple mathematical models can reveal deeper insights into group dynamics and collective intelligence.
The P-Beauty game serves as a metaphor for broader social phenomena, particularly in the context of repeated games. For instance, the game can be used to analyze political strategies, where parties adjust their positions to appeal to the median voter, often leading to polarization. This reflects how individuals or groups may shift their strategies over time in response to others, seeking to maximize their advantage while considering the behavior of their competitors.
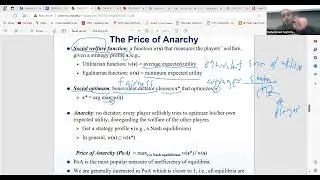
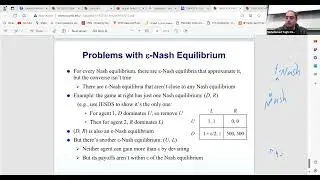
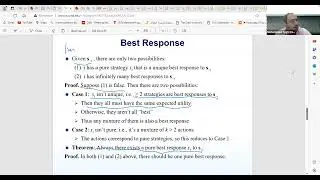
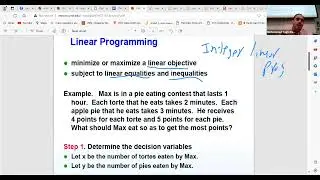
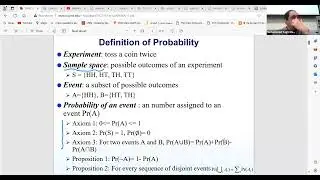
The class also introduced the concept of Pareto optimality and its significance in game theory. We explored examples of Pareto optimal strategies, emphasizing that in common payoff games, all players receive the same outcome for a given strategy. The discussion set the stage for a deeper exploration of Nash equilibrium in future sessions, highlighting the complexity and richness of solution concepts in game theory.
#GameTheory, #PBeautyGame, #SocialBehavior, #PoliticalStrategy, #ParetoOptimality, #NashEquilibrium, #GroupDynamics, #DecisionMaking, #MathematicalModels, #CollectiveIntelligence, #ComputationalGameTheory, #StrategicAgents, #ComputationalStrategies, #SelfishAgents, #MathematicalModeling, #ProblemSolving, #AdvancedComputing,#Mathematics, #Algorithms
