Lesson 11: Computational Game Theory by Mohammad Hajiaghayi: Price of Anarchy and Braess's Paradox
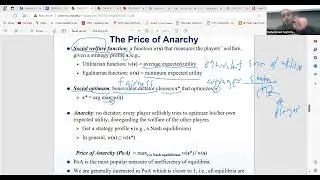
In this session, we talk about Price of Anarchy (PoA) and Braess's Paradox. The "price of anarchy" refers to the inefficiency that arises when individual agents in a system act selfishly, without central coordination, leading to suboptimal outcomes. This concept contrasts with a more controlled or centralized system, such as one governed by a dictator or central authority, where decisions aim to maximize overall benefit. The challenge is to measure how much worse the outcome in a self-organized, anarchic system can be compared to a centrally optimized solution. Game theory is often used to quantify this inefficiency, focusing on how selfish behavior affects the collective good.
Several real-world examples demonstrate the price of anarchy in action, particularly in traffic networks. When individuals make decisions based on their own convenience, traffic flow can worsen, even when additional infrastructure, such as new roads or lanes, is introduced. Famous examples include the Stuttgart paradox, where opening new roads led to worse traffic, and the closure of parts of Broadway in New York, which improved traffic flow. These paradoxical situations illustrate how decentralized decision-making can sometimes make conditions worse rather than better.
The price of anarchy is not limited to physical networks; it also applies to digital communication networks where computers, like selfish agents, choose routes that seem optimal but may congest the overall system. The study of this phenomenon in game theory helps to reveal the hidden consequences of decentralized systems and informs better design and policy decisions in various fields. This framework is crucial for understanding when and why attempts to improve a system might backfire.
#PriceOfAnarchy, #GameTheory, #TrafficParadox, #SelfishAgents, #NashEquilibrium, #CentralizedControl, #DictatorshipVsDemocracy, #SystemInefficiency, #NetworkOptimization, #GameTheory, #StrategicDecisionMaking, #PriceOfAnarchy, #MixedStrategies, #DominatedStrategies, #Optimization, #AlgorithmicComplexity, #BraessParadox
![[Unboxing]C.P. company basic summer items for holiday trip!](https://images.videosashka.com/watch/ChdcmiA7WhE)
