Lesson 10: Computational Game Theory by Mohammad Hajiaghayi: Ɛ-Nash Equilibria and Dominant Strategy
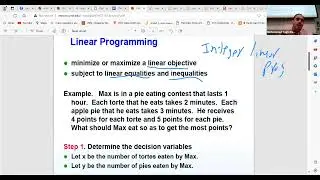
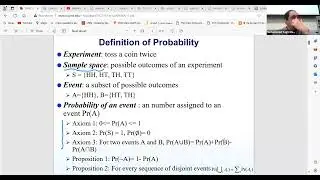
In this session, we talk about Ɛ-Nash equilibria and dominant strategies in games. More precisely, we revisit the concept of Nash Equilibrium (Nash EQ) and its computational complexity, introducing the idea of Epsilon Nash Equilibrium. Epsilon Nash offers a practical approach to understanding strategic decision-making, where players are satisfied with their current strategies as long as the gain from switching is minimal, represented by a small value, Epsilon. This concept acknowledges the cost of changing strategies and asserts that an Epsilon Nash EQ always exists for any positive Epsilon, making it a useful tool in situations where finding an exact Nash EQ is challenging.
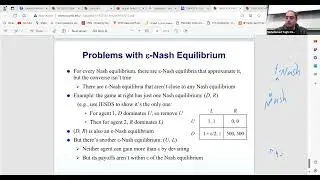
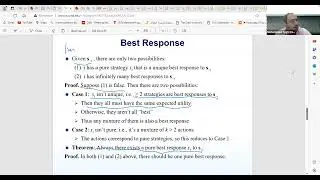
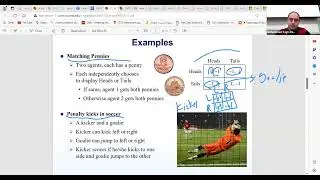
The discussion then shifts to the relationship between Epsilon Nash and pure Nash Equilibrium. While Nash EQ is stable, it doesn’t always optimize the overall utilities of all players. The session highlights that although Epsilon Nash EQ can be easier to compute, it may not always be close to the actual Nash EQ. The complexity lies in whether Epsilon Nash can approximate the true Nash EQ effectively, especially in games where mixed strategies are involved. The lecture also touches on dominated strategies, considering how strictly and weakly dominated strategies influence the stability of the equilibrium.
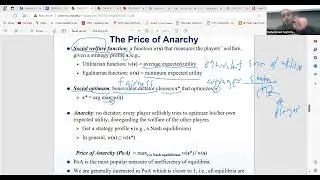
Finally, the concept of the Price of Anarchy is introduced, which measures how much is lost in utility when players act selfishly in Nash Equilibrium compared to an optimal solution that maximizes the sum of all players’ utilities. This ties into the broader goal of finding not just any stable settlement but one that also optimizes the overall outcomes for all players involved. The session concludes with a teaser for the next discussion on Braess’s Paradox, which will delve into the counterintuitive results that can arise in strategic games.
#NashEquilibrium, #EpsilonNash, #GameTheory, #StrategicDecisionMaking, #PriceOfAnarchy, #MixedStrategies, #DominatedStrategies, #Optimization, #AlgorithmicComplexity, #BraessParadox