Lesson 3: Computational Game Theory by Mohammad Hajiaghayi: Introduction to Probability Theory Part2
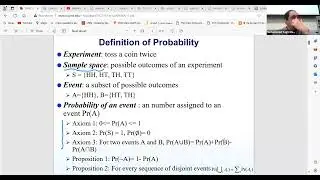
In this session, we continue discussing basics of probability theory which is very important in game theory. In our recent session, we revisited conditional probability and its significance in Game Theory. Conditional probability helps us understand the likelihood of an event given that another event has already occurred. This concept is crucial because events that might seem independent can exhibit dependencies when additional information is considered. For instance, we explored how two events, A and B, might be independent under normal circumstances but could become dependent when conditioned on a third event, C. This shift in dependency highlights how new information can alter our understanding of events and their relationships.
We also discussed the Bayes' Theorem, a fundamental principle in probability that provides a way to update the probability of a hypothesis as more evidence or information becomes available. This theorem is particularly useful in a wide range of applications, from medical diagnoses to spam filtering and even in strategic decision-making scenarios in Game Theory. Understanding Bayes' Theorem is essential for analyzing situations where probabilities are influenced by prior knowledge or new data, making it a key tool for navigating complex systems.
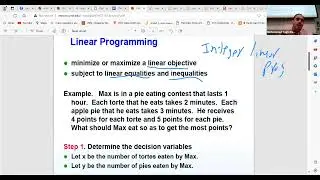
Additionally, we touched on various probability distributions, such as the normal (Gaussian) distribution and the Poisson distribution, both of which are integral to modeling and understanding random variables and their behaviors. The normal distribution is ubiquitous in natural phenomena and is known for its symmetric bell-shaped curve. In contrast, the Poisson distribution is used for events that occur independently and sporadically over time. Mastery of these distributions and their properties is vital as we move towards more advanced topics like linear programming and convex optimization, which are indispensable tools in the study of Game Theory.
#GameTheory, #ComputationalGameTheory, #StrategicAgents, #ComputationalStrategies, #SelfishAgents, #ConditionalProbability, #BayesTheorem, #ProbabilityDistributions, #NormalDistribution, #PoissonDistribution, #StrategicDecisionMaking, #MathematicalModeling, #LinearProgramming, #ComplexSystems, #ProbabilityTheory, #ABTesting, #Mathematics, #Algorithms, #ConditionalIndependence