Lesson 9: Computational Game Theory by Mohammad Hajiaghayi: Finding Nash Equilibria
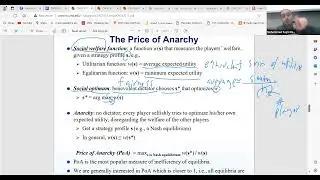
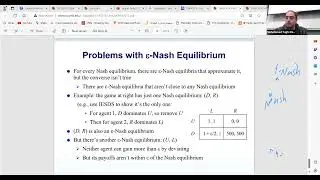
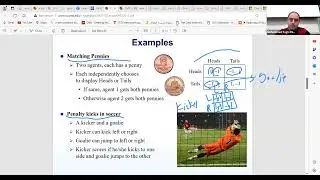
In this session, we discuss different algorithms for finding Nash equilibria. In particular, we continue our analysis of games, focusing on the tools and concepts essential for understanding game theory. We discuss solution concepts, which are stable situations or settlements between players, and dive deeper into Pareto optimality, a strategy profile where no player can be made better off without making another worse off. The session also introduces the Nash equilibrium, specifically focusing on mixed Nash equilibria, where strategies are distributions over possible actions, making the discussion more complex and exciting.
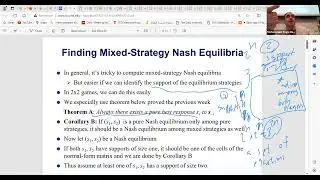
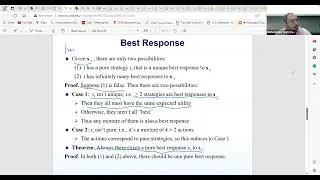
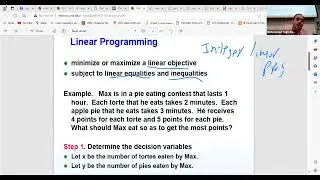
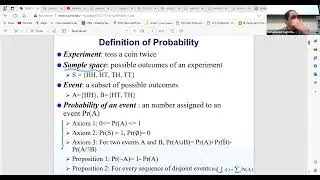
We explore how to find mixed Nash equilibria by identifying the support of equilibrium strategies. The support consists of actions with nonzero probabilities, and determining them involves considering all possible subsets of actions, which can be computationally intense. For two-player games, we discuss the historical methods used to solve these equilibrium equations, including linear programming, which provides a general approach to finding solutions by solving a system of inequalities.
The session also touches on the complexity of finding Nash equilibria, explaining that while Nash's original concept falls into a class of problems called "PPAD," its exact computational complexity remains an open question. This leads to a broader discussion about the significance of understanding P versus NP problems in computer science, emphasizing their importance for students and researchers alike. The lecture highlights the ongoing challenges and opportunities in game theory, leaving the door open for further exploration in future sessions.
#GameTheory, #NashEquilibrium, #MixedStrategies, #ParetoOptimality, #SolutionConcepts, #LinearProgramming, #PPAD, #ComputationalComplexity, #PvsNP, #StrategicAnalysis