Lesson 8: Computational Game Theory by Mohammad Hajiaghayi: Best Response and Nash Equilibrium
In this session, we talk about best responses in a game and the concept of Nash equilibrium.
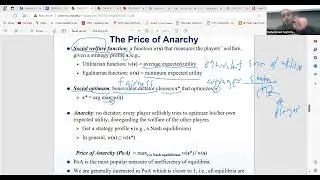
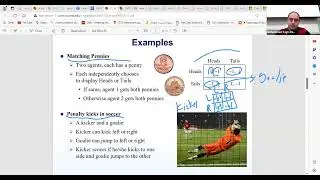
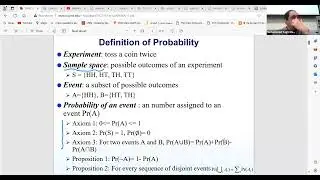
In particular, we delve into normal form games and the foundational motivations behind game theory, highlighting how many games can be represented in this formal structure. We discuss the distinction between single-player optimization strategies and multi-player games, where the need for stable solutions, or "solution concepts," arises due to the interactions between players. In particular, we explore zero-sum games, where one player's gain equals another's loss, and introduce the concept of Pareto optimality, where a strategy profile is considered optimal if no other profile can improve one player's outcome without worsening another's.
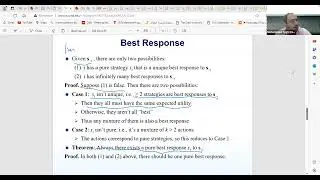
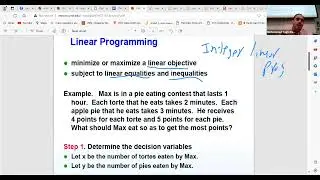
We also examine the idea of a best response, which is essentially an optimal strategy for a player, given the strategies of all other players. This concept is crucial in understanding how players might act in games with multiple participants, where each player seeks to maximize their own utility. The session covers the notation and mechanics of best response strategies, emphasizing how they relate to both pure and mixed strategies in different game scenarios.
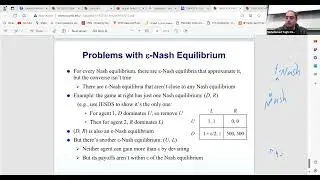
Finally, we discuss the Nash equilibrium, an important solution concept in game theory, where no player has an incentive to deviate from their strategy given the strategies of others. We explain the difference between strong and weak Nash equilibria, noting that weak equilibria are less stable because they allow for multiple best responses. The session sets the stage for future discussions on more complex games and examples, including those with no pure Nash equilibrium, highlighting the practical challenges and theoretical depth of game theory.
#GameTheory, #NormalFormGames, #ZeroSumGames, #ParetoOptimality, #BestResponse, #NashEquilibrium, #PureStrategies, #MixedStrategies, #SolutionConcepts, #StrategicInteractions