Lesson 20: Algorithmic Lower Bounds by Mohammad Hajiaghayi: PCP Theorem for Approximation Hardness 2
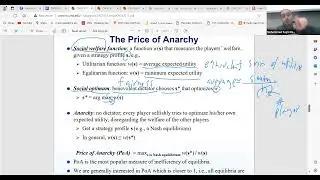
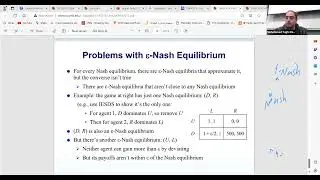
In this session guest lecturer Prof. Bill Gasarch continues talking about PCP theorem for approximation hardness. The class delves into clarifying a point about whether the PCP theorem implies P=NP. The instructor presents slides to illustrate why the PCP theorem does not directly imply P=NP, addressing the limitations of running all possible oracles. The discussion shifts to various problems, including jigsaw puzzles, three-dimensional matching, and the traveling salesman problem (TSP), emphasizing their hardness to approximate. In the latter part of the class, the instructor covers several problems that are hard to approximate, such as three-dimensional matching and the traveling salesman problem (TSP). The hardness results for Max 3SAT are highlighted, leading to the conclusion that the TSP problem cannot be arbitrarily well-approximated.
#ApproximationAlgorithms, #PCPTheorem, #P=NP, #Hardness, #JigsawPuzzle, #TSP, #Max3SAT, #MathematicalChallenges, #AlgorithmDesign, #ComputationalComplexity, #TheoreticalComputerScience, #AlgorithmicLowerBounds
All handwritten lecture notes for this course are available through the website of the instructor
at http://www.cs.umd.edu/~hajiagha/ALB19... (Just click on the "Algorithmic Lower Bounds: Fun with Hardness Proofs" course from the website).
The BOOK for the course entitled "Computational Intractability: A Guide to Algorithmic Lower Bounds" by Demaine, Gasarch, and Hajiaghayi is freely available at https://hardness.mit.edu/