Lesson 19: Algorithmic Lower Bounds by Mohammad Hajiaghayi: PCP Theorem for Approximation Hardness 1
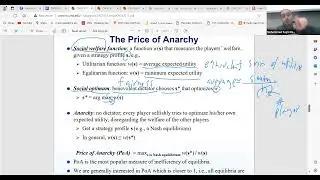
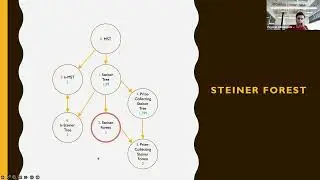
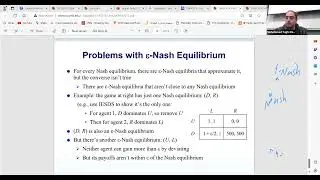
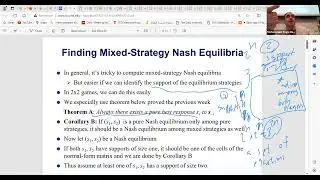
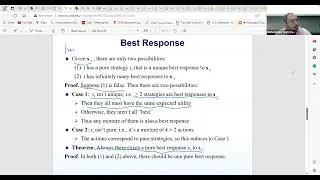
In this session guest lecturer Prof. Bill Gasarch talks about PCP theorem for approximation hardness. The class dives into the topic of approximation algorithms, specifically discussing minimization and maximization problems, including min rep and Max rep, which are crucial for Unique game and PCP theorem. The instructor mentions the use of the PCP theorem as a black box to prove lower bounds on approximation and highlights the complexity involved in proving the theorem. In the later part of the recording, the discussion shifts to the concept of approximation algorithms and the role of the PCP theorem in proving lower bounds. The instructor introduces the idea of differentiating between large and small clicks in approximation algorithms, emphasizing the significance of the gap between these two scenarios. A question is raised about the optimality of the parameters, and the instructor clarifies that subsequent research has provided better results, indicating that the current parameters are not optimal. The class ends with a reminder of upcoming sessions and a farewell. The class concludes with a preview of upcoming topics and an acknowledgment of the challenges and breakthroughs associated with the PCP theorem.
#ApproximationAlgorithms, #PCPTheorem, #Minimization, #Maximization, #UniqueGame, #AlgorithmComplexity, #BlackBoxTheorem, #LowerBounds, #MathematicalChallenges, #AlgorithmDesign, #ComputationalComplexity, #TheoreticalComputerScience, #AlgorithmicLowerBounds
All handwritten lecture notes for this course are available through the website of the instructor
at http://www.cs.umd.edu/~hajiagha/ALB19... (Just click on the "Algorithmic Lower Bounds: Fun with Hardness Proofs" course from the website).
The BOOK for the course entitled "Computational Intractability: A Guide to Algorithmic Lower Bounds" by Demaine, Gasarch, and Hajiaghayi is freely available at https://hardness.mit.edu/