Lesson 23: Algorithmic Lower Bounds by Mohammad Hajiaghayi: Fixed-Parameter Algorithm Lower Bounds 3
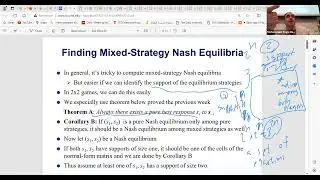
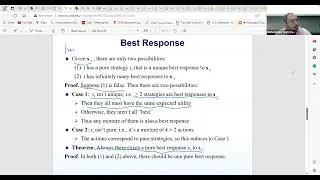
In this session we recap parameterized complexity and fixed-parameter algorithm lower bounds. First we discuss the hardness results for k-clique and k-independent set problems, emphasizing the absence of efficient algorithms under certain assumptions such at ETH, defined in the lecture. A stronger result is introduced, indicating that under ETH conjecture, no n^f(K) algorithm exists for K-clique.
The instructor delves into the proof of this assertion, outlining the assumptions and implications. Discussions revolve around the reduction of problems such as vertex cover, independent set, and dominating set, showcasing the intricate relationship between fixed parameter algorithms and computational assumptions. The session explores the complexity of these problems and highlights the significance of ETH conjecture in determining algorithmic efficiency.
Concluding the session, the instructor summarizes the findings and encourages further exploration of related topics. The importance of parameterization in various computational domains, including streaming and approximation algorithms, is emphasized.
#ETH, #FixedParameterAlgorithms, #AlgorithmicGoals, #MulticoloredClique, #VertexCover, #ParameterizedReduction, #DominatingSet, #Hardness, #PolynomialTime, #ParameterizedProblems, #ComputationalAssumptions, #ExponentialTimeHypothesis, #complexity, #ComplexityTheory, #Integers, #SubsetDivision, #Foundations, #Scheduling, #StreamingAlgorithms, #ApproximationAlgorithms, #MathematicalChallenges, #AlgorithmDesign, #ComputationalComplexity, #TheoreticalComputerScience, #AlgorithmicLowerBounds
All handwritten lecture notes for this course are available through the website of the instructor
at http://www.cs.umd.edu/~hajiagha/ALB19... (Just click on the "Algorithmic Lower Bounds: Fun with Hardness Proofs" course from the website).
The BOOK for the course entitled "Computational Intractability: A Guide to Algorithmic Lower Bounds" by Demaine, Gasarch, and Hajiaghayi is freely available at https://hardness.mit.edu/