Lesson 7: Network Algorithms and Approximations by Mohammad Hajiaghayi: FRT Embeddings into Trees
In this session, we discuss Fakcharoenphol, Rao, and Talwar (FRT) algorithm and its analysis of metric embeddings into probabilistic trees.
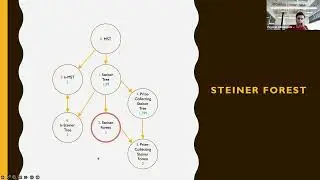
First we focus on the group Steiner tree problem, a generalization of the Steiner tree problem with applications in network design and VLSI chip design. In the group Steiner tree problem, the goal is to find a minimum-cost tree that connects at least one terminal from each group in a collection of terminal groups. The session discusses the problem's definition, applications, and the challenges in designing efficient approximation algorithms.
The session also explores various approaches to solving the group Steiner tree problem, including linear programming relaxations and the primal-dual method. It discusses the limitations of these approaches and the inherent complexity of the problem, particularly in achieving tight approximation guarantees.
The session also touches on the concept of probabilistic embedding into trees, a technique used to simplify network problems by approximating graph metrics with tree metrics. This approach involves embedding the graph into a distribution of trees and solving the problem on each tree, taking the minimum solution as the final result. The session discusses the benefits and limitations of this approach, particularly for the group Steiner tree problem.
Overall, the session provides a comprehensive overview of the group Steiner tree problem, its applications, and the challenges in designing efficient approximation algorithms. It highlights the importance of this problem in network design and its connection to other related problems in the field.
#groupsteinertree, #steinertree, #networkdesign, #approximationalgorithms, #linearprogramming, #primaldual, #probabilisticembedding, #treeapproximation, #optimization, #combinatorialoptimization, #VLSIchipdesign, #graphalgorithms