Lesson 17: Algorithmic Lower Bounds by Mohammad Hajiaghayi: Massively Parallel Comput Lower Bounds 2
In this session guest lecturer, Jan Olkowski continues talking about the Massively Parallel Computation (MPC) model covering both upper and lower bounds. The lecture delves into the MPC model, emphasizing its rounds, number of machines, and their ability to store a limited number of bits. Jan introduces the shuffle model, equating it with the behavior of MPC but in a more formal and easily provable manner for lower bounds. The discussion explores functions computable in the shuffle model, focusing on polynomials and their maximum degrees.
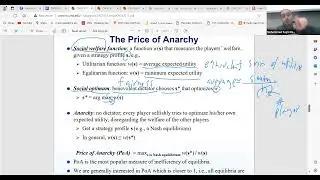
The lecture also touches on conditional hardness assumptions, particularly the conjecture that connectivity in MPC requires at least logarithmic rounds based on the graph's diameter. Conditional on this assumption, Jan demonstrates the lower bounds for other problems, such as maximal matching, synchronous orientation, and Delta Square vertex coloring. The session concludes with a mention of ongoing research and the possibility of obtaining more knowledge about the solvability of problems under such assumptions.
#MPC, #ShuffleModel, #UpperBounds, #LowerBounds, #Polynomials, #Connectivity, #ConditionalHardness, #MaximalMatching, #SynchronousOrientation, #VertexColoring, #GraphTheory, #Algorithms, #BigData, #ComputationalModels, #MathematicalChallenges, #AlgorithmDesign, #ComputationalComplexity, #TheoreticalComputerScience, #AlgorithmicLowerBounds
All handwritten lecture notes for this course are available through the website of the instructor
at http://www.cs.umd.edu/~hajiagha/ALB19... (Just click on the "Algorithmic Lower Bounds: Fun with Hardness Proofs" course from the website).
The BOOK for the course entitled "Computational Intractability: A Guide to Algorithmic Lower Bounds" by Demaine, Gasarch, and Hajiaghayi is freely available at https://hardness.mit.edu/