Lesson 18: Algorithmic Lower Bounds by Mohammad Hajiaghayi: Approximability and Inapproximability
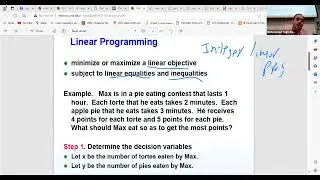
In this session we talk about approximability and inapproximability in particular label cover problem. In particular we discuss approximation algorithms, focusing on both minimization and maximization problems and their approximability. The instructor introduces the concept of fixed-parameter algorithms, highlighting their exponential running time but potential practicality for problems with a small parameter.
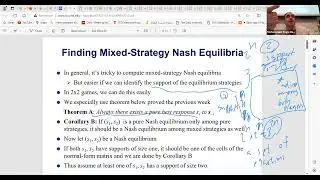
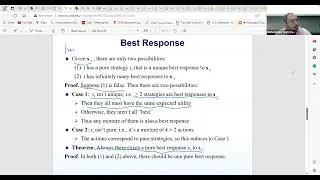
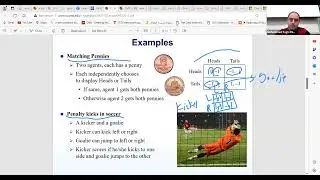
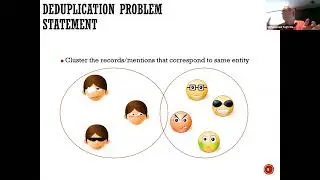
The discussion delves into various maximization and minimization problems, including set cover, label cover, max rep, and min rep. The instructor emphasizes the relevance of comparing a given problem's hardness to well-known problems in order to understand its complexity better.
#ApproximationAlgorithms, #Minimization, #Maximization, #FixedParameterAlgorithms, #SetCover, #LabelCover, #MaxRep, #MinRep, #HardnessResults, #MathematicalChallenges, #AlgorithmDesign, #ComputationalComplexity, #TheoreticalComputerScience, #AlgorithmicLowerBounds
All handwritten lecture notes for this course are available through the website of the instructor
at http://www.cs.umd.edu/~hajiagha/ALB19... (Just click on the "Algorithmic Lower Bounds: Fun with Hardness Proofs" course from the website).
The BOOK for the course entitled "Computational Intractability: A Guide to Algorithmic Lower Bounds" by Demaine, Gasarch, and Hajiaghayi is freely available at https://hardness.mit.edu/