Lesson 21: Algorithmic Lower Bounds by Mohammad Hajiaghayi: Fixed-Parameter Algorithm Lower Bounds 1
In this session we talk about parameterized complexity and fixed-parameter algorithm lower bounds. First, the instructor provides an overview of the course content so far, including discussions on NP hardness, streaming approximation algorithms, and fine grain complexity. The upcoming topic is introduced as fixed-parameter algorithms and lower bounds for parameterized problems, with an emphasis on defining the important concepts.
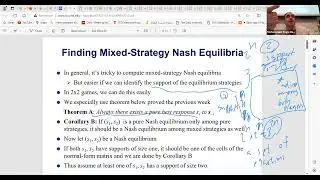
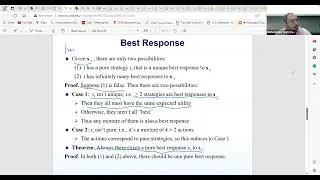
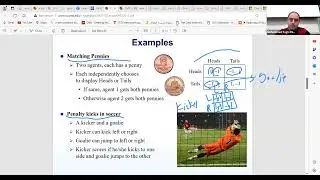
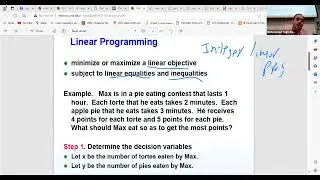
Algorithmic goals are discussed, emphasizing the desire to design algorithms for correct and fast solutions for hard problems. Various scenarios are explored, including situations where only two out of the three goals can be achieved simultaneously. Examples are provided, such as the matching problem for correct and fast solutions, and approximation algorithms for near-optimal solutions. The concept of fixed-parameter algorithms is introduced as a solution for obtaining correct solutions to hard problems within polynomial time.
The session concludes with a discussion on the multicolored clique problem and its equivalence to traditional clique problems. The instructor elaborates on the use of multicolored clique to prove hardness results and concludes the class by highlighting future topics
#FixedParameterAlgorithms, #AlgorithmicGoals, #MulticoloredClique, #Hardness, #PolynomialTime, #ParameterizedProblems, #complexity, #ComplexityTheory, #Integers, #SubsetDivision, #Foundations, #Scheduling, #MathematicalChallenges, #AlgorithmDesign, #ComputationalComplexity, #TheoreticalComputerScience, #AlgorithmicLowerBounds
All handwritten lecture notes for this course are available through the website of the instructor
at http://www.cs.umd.edu/~hajiagha/ALB19... (Just click on the "Algorithmic Lower Bounds: Fun with Hardness Proofs" course from the website).
The BOOK for the course entitled "Computational Intractability: A Guide to Algorithmic Lower Bounds" by Demaine, Gasarch, and Hajiaghayi is freely available at https://hardness.mit.edu