Lesson 8: Network Algorithms and Approximations by Mohammad Hajiaghayi: Network Design Problems
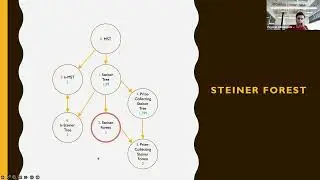
In this session, we talk about different network design problems, in particular Steiner tree, Steiner forest, and buy-at-bulk.
First we focus on the buy-at-bulk network design problem, a generalization of the Steiner forest problem where the cost of buying bandwidth or capacity on edges satisfies economies of scale. The problem involves meeting demands between pairs of nodes in a network by installing sufficient capacity on edges, with the cost of bandwidth typically decreasing per unit as the amount of bandwidth purchased increases.
The session discusses the concept of economies of scale, where buying in bulk leads to cost savings, and how it applies to network design problems. It also explores the connection between the buy-at-bulk problem and the cost-distance problem, where the cost of an edge depends on both its installation cost and the length of the path it represents.
The session also covers the generalization of the buy-at-bulk problem to include non-uniform costs and sub-additive functions, which model more complex cost structures. It discusses the challenges in designing approximation algorithms for these problems, particularly in achieving poly-logarithmic approximation guarantees.
Finally, the session touches on the single-source case, where all demands originate from a single node, and the uniform case, where the cost and length functions are the same on all edges. It also discusses the use of techniques like probabilistic embedding into trees and the primal-dual method to address these problems.
#buyatbulk, #networkdesign, #Steinerforest, #economiesofscale, #costdistance, #approximationalgorithms, #probabilisticembedding, #primaldual, #optimization, #combinatorialoptimization, #graphalgorithms, #networkoptimization