Adaptive neural control of a 3 DOF helicopter with unknown time delay
Title: - Adaptive neural control of a 3-DOF helicopter with unknown time delay
---------------------------------------------------------------------------
Implementation Plan:
----------------------
Scenario 1:
------------
Step 1: Initially, we designed the 3DOF helicopter simulink model.
Step 2: Next, we NN technique is utilised, In this step the helicopter NN approximation error and the time-varying external disturbance, an adaptive parameter is designed by resorting to a hyperbolic tangent function.
Step 3: Next, we perform a NN-based fault tolerant control scheme, In this step, a fault-tolerant controller is designed by combining back-stepping with NN techniques. In order to obtain the derivatives of virtual control inputs when employing backstepping techniques.
Step 4: Next, Stability analysis process, In this section, one theorem is given. Specifically, the proof that the convergence of variables.
4.1 : Theorem : For a variable designed as Equation with a variable designed as Equation, when the parameter is chosen properly, and the tracking error is ensured to be bounded, then, the convergence of the variable can guarantee the convergence of tracking error.
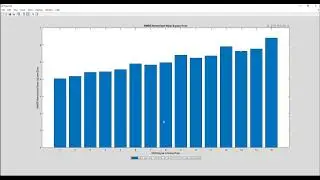
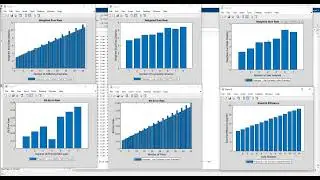
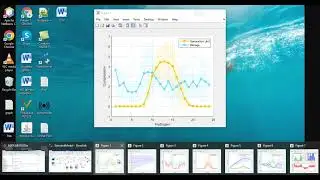
Step 5: The proposed research work is evaluated with the performance metrics,
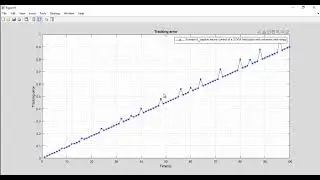
• Time(s) vs. Tracking error
• Time(s) vs. Control input
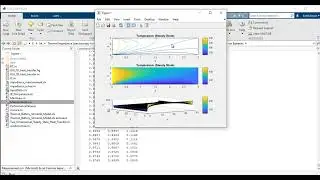
• Time(s) vs. Pitch angle(deg)
• Time(s) vs. Elevation angle(deg)
================================================================================================================================================================
Scenario 2:
--------------
Step 1: Initially, we designed the 3DOF helicopter simulink model.
Step 2: Next, we NN technique is utilised, In this step the helicopter NN approximation error and the time-varying external disturbance, an adaptive parameter is designed by resorting to a hyperbolic tangent function.
Step 3: Next, we perform a NN-based fault tolerant control scheme, In this step, a fault-tolerant controller is designed by combining back-stepping with NN techniques. In order to obtain the derivatives of virtual control inputs when employing backstepping techniques.
Step 4: Next, Stability analysis process, In this section, another theorem is given. Specifically, the proof that the convergence of variables.
4.1: Theorem : Consider a 3-DOF helicopter described as Equations with system uncertainties, external time-varying disturbances and actuator faults. When the virtual control inputs are designed as Equations the control inputs are designed as Equations and the adaptive updating laws are designed as Equations then, the closed-loop system is stable, and the tracking errors and approximation errors can converge to their corresponding compact sets.
Step 5: The proposed research work is evaluated with the performance metrics,
• Time(s) vs. Tracking error
• Time(s) vs. Control input
• Time(s) vs. Pitch angle(deg)
• Time(s) vs. Elevation angle(deg)
==============================================================================================================================================================
Software Requirement:
-----------------------
1. Tool: Matlab R2020a/Simulink
2. Operating System: Windows 10-(64-bit)
=================================================================================================================================================================
