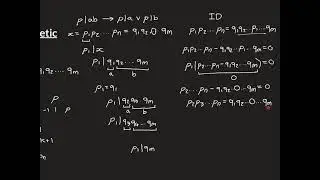Bezout’s Identity
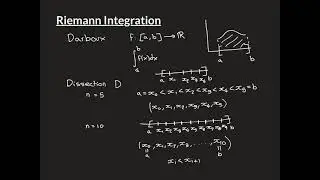
Bezout’s Identity also called Bezout’s lemma is the name for the fact that if m and n are integers and d = gcd(m,n), then there exists integers x and y such that xm + yn = d.
This fact is used in many proofs in number theory.
In this video we show how the proof of this comes from the euclidean algorithm and show how you can use the euclidean algorithm to find a specific x and y which satisfy this.
This is called the extended euclidean algorithm.
We give several examples of this throughout the video.