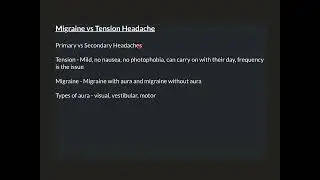
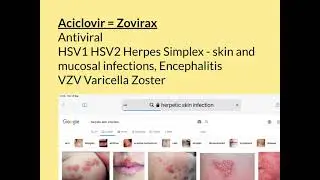
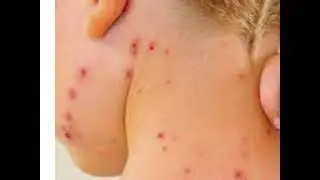
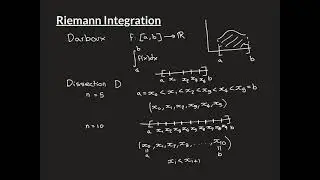
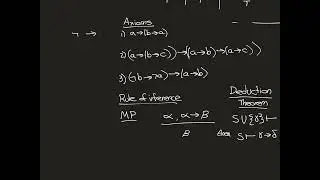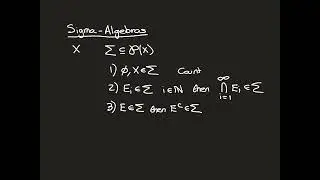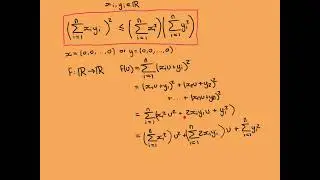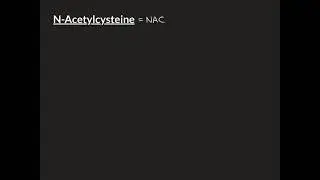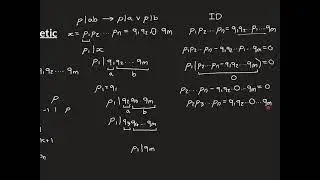Euclid’s Lemma
Euclid’s lemma is an important result in number theory.
It states that if a prime number p divides a product ab of two integers a and b then it must divide at least one of the two integers that makes that product.
The proof of this uses bezout’s identity.
We will use Euclid’s Lemma in a subsequent video to prove the fundamental theorem of arithmetic.