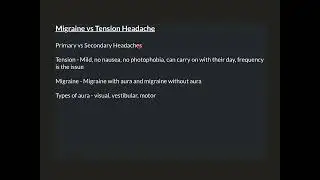
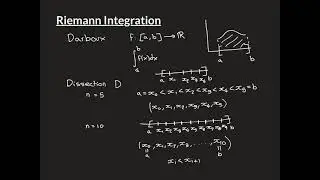
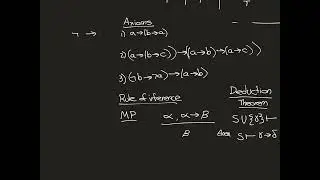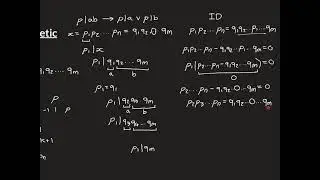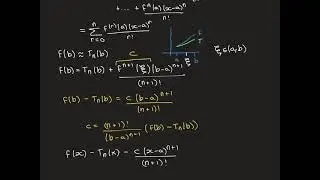The Fundamental Theorem of Arithmetic
The fundamental theorem of arithmetic is also called the prime factorisation theorem and the unique factorisation theorem.
It states that for any positive integer greater than or equal to 2, that the number is either prime itself or it can be written as the product of prime numbers.
This product of primes is known as the prime factorisation of the number.
The theorem goes further and says that not only does the prime factorisation exist but that it is also unique up to rearrangement of the order that the primes appear in the product.
In this video we prove this. The proof relies on Euclid’s Lemma. So please be familiar with this before watching.