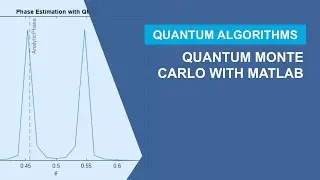
Quantum Monte Carlo (QMC) with MATLAB
Monte Carlo methods are widely applied in fields such as engineering, physics, and finance. Quantum Monte Carlo (QMC) enhances the traditional Monte Carlo approach by leveraging quantum computing features. In this demonstration, you’ll learn how to calculate the mean of the trigonometric function (\sin^2 x), where (x) follows a normal distribution. Begin by performing this calculation analytically, then employ the classic Monte Carlo method.
In the QMC methodology, you first load the probability distribution of the variable (x) onto 5 qubits using entanglement. Next, encode the expected value of the random variable onto a single value qubit. Finally, use the quantum phase estimation module to determine the mean encoded on the value qubit.
Ultimately, when you compare the means obtained from each method, you will find that they are consistent across approaches.
Related information:
Quantum Computing with MATLAB: https://bit.ly/3zyLNEK
Quantum Monte Carlo (QMC) Simulation: https://bit.ly/3zQhp9n
Introduction to Quantum Computing: https://bit.ly/3zyJ9ir
--------------------------------------------------------------------------------------------------------
Get a free product trial: https://goo.gl/ZHFb5u
Learn more about MATLAB: https://goo.gl/8QV7ZZ
Learn more about Simulink: https://goo.gl/nqnbLe
See what's new in MATLAB and Simulink: https://goo.gl/pgGtod
© 2024 The MathWorks, Inc. MATLAB and Simulink are registered trademarks of The MathWorks, Inc.
See www.mathworks.com/trademarks for a list of additional trademarks. Other product or brand names may be trademarks or registered trademarks of their respective holders.
