TI-83/84: Chi square critical values using Solver and X2cdf
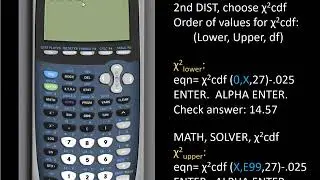
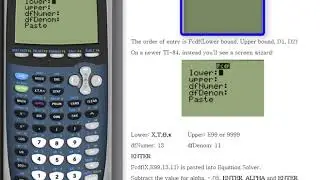
The TI-83/84 doesn't have a chi square inverse function, so when we need to get chi square critical values, we can use the Solver function combined with chi square cdf and tell the calculator to solve for the "X" chi square value that has some area to the left or right of it. All we need to know are the confidence level or alpha, and the n or df.
In the video, I show the example of finding lower and upper critical values for a confidence interval. The area we subtract when we solve for chi square is (1-conf level)/2. For a two-tailed hypothesis test, we would instead subtract alpha/2. For a one-tailed hypothesis test, we subtract alpha.
Basically, we set up the equation to solve for the X which either has some area between 0 and chi square, or to solve for the X which has some area between chi square and infinity to the right.