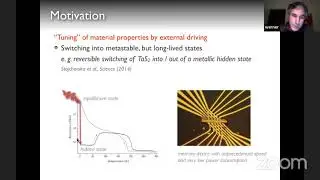
G. Vignale: "Quantum continuum mechanics and quantum incompressibility of electron-hole bilayers"
Quantum continuum mechanics (QCM) is a theory that allows a relatively simple calculation of the excitation energies of a many-body system in terms of its ground state properties. We have applied this theory to the study of the excitation spectrum of a two-dimensional electron-hole system, in which electrons and holes reside in well-separated layers of a semiconductor heterostructure. The theory predicts the existence of a gap for excitations in the charged channel. This gap exists for all densities and interlayer distances and does not require broken translational invariance or BCS-like pairing. However, a completely independent calculation based on BCS mean field theory gives a qualitatively similar result. An immediate consequence of the gap is that the static density-density response function of the charged channel vanishes as q2 for wave vector q0, rather than linearly in q, as commonly expected. In this sense, the system is incompressible. This feature, which has no analog in the classical electron-hole plasma, implies the existence of a discontinuity in the chemical potential of electrons and holes when the numbers of electrons and holes are equal. Recent capacitance measurements on electron-hole bilayers in the transition metal dichalcogenide heterostructure MoSe2/WSe2 (https://arxiv.org/abs/2104.05066) confirm this discontinuity, showing that the fluid is exciton-compressible but charge- incompressible – which agrees with the QCM description and is consistent with the presence of an excitonic insulator. It should be experimentally observable by monitoring the densities of electrons and holes in response to potentials that attempt to change these densities in opposite directions.