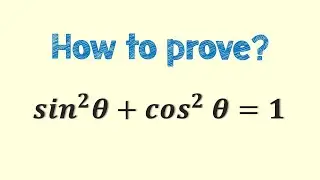Simple Curve Closed Curve Definition Examples Not Simple Difference Class 8🔥
In this video, we will explore the difference between simple curve, not a simple curve, simple closed curve, and not a simple closed curve. These are terms used in geometry to describe the properties of curves in two-dimensional space. Understanding these concepts is important in various fields such as computer graphics, robotics, and physics.
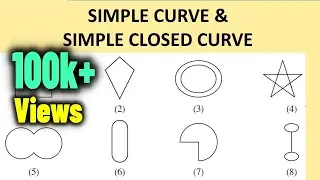
A simple curve is a curve that does not intersect itself. In other words, if you take any two points on the curve, there is only one path between them that stays on the curve. Examples of simple curves include straight lines, circles, and parabolas. A simple curve can be open, meaning that it extends to infinity in one or both directions, or closed, meaning that it forms a loop.
A not a simple curve, also known as a self-intersecting curve, is a curve that intersects itself at one or more points. Examples of not a simple curve include figure eight curves and the infinity symbol. A not a simple curve can be open or closed, but it cannot be simple.
A simple closed curve is a closed curve that does not intersect itself. Examples of simple closed curves include circles, ellipses, and rectangles. A simple closed curve divides the plane into two regions, an interior region and an exterior region. The interior region is the region inside the curve, while the exterior region is the region outside the curve.
A not a simple closed curve, also known as a self-intersecting closed curve, is a closed curve that intersects itself at one or more points. Examples of not a simple closed curve include the lemniscate of Bernoulli and the trefoil knot. A not a simple closed curve divides the plane into several regions, with some of them being the interior and some of them being the exterior. The number of regions depends on the number and location of the self-intersections.
It is important to note that the terminology "simple" does not imply that a curve is easy to work with or understand. For example, the circle, which is a simple curve, has properties that can be difficult to analyze and understand, such as its curvature and circumference. On the other hand, not a simple curve, such as the lemniscate of Bernoulli, can have elegant and interesting properties.
Understanding the properties of curves is important in many fields. For example, in computer graphics, curves are used to create smooth shapes in 3D modeling and animation. In robotics, curves are used to describe the paths of robots and their end-effectors.
In physics, curves are used to describe the motion of objects and the shape of space-time in general relativity. Understanding the difference between simple curve, not a simple curve, simple closed curve, and not a simple closed curve is important for correctly interpreting and analyzing geometric data in these fields.
In this video, we will explore these concepts in detail, including examples and visualizations. We will also discuss how to determine whether a given curve is simple or not, and how to identify the self-intersection points of a not a simple curve or not a simple closed curve. Additionally, we will discuss some of the applications of these concepts in various fields.
By the end of this video, you will have a clear understanding of the difference between simple curve, not a simple curve, simple closed curve, and not a simple closed curve. You will also understand why these concepts are important and how they are used in different fields. Whether you are a student, a researcher, or simply curious about geometry, this video will provide you with a comprehensive and engaging introduction to these important concepts.
0:00 - What is curve?
0:10 - Definition of Simple Curve.
0:19 - Definition of not a simple curve.
0:27 - Definition of simple closed curve.
0:40 - Definition of "not a simple closed curve".
1:06 - Examples Question.
Diagram of open curve and closed curve
• Open Curve and Closed Curve Diagram 4...
#simplecurve, #simpleclosedcurvedefinition, #simpleclosedcurve, #simplecurvedefinition, #asimpleclosedcurve, #simplecurvethatisnotclosed, #simplecurveexamples, #aclosedcurvethatisnotsimple, #simplecurveandsimpleclosedcurve, #aisasimpleclosedcurve,
#differencebetweensimplecurveandsimpleclosedcurve, #notasimplecurve, #definesimpleclosedcurve,