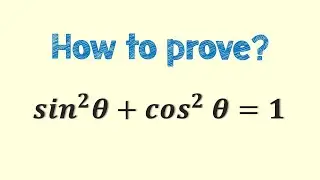Symmetry of a Graph about y axis, x axis, and origin || How to test for symmetry of Function
Symmetry of a Graph about y axis, x axis, and origin and how to test it? In this video you will learn the three basic types of symmetry which are symmetric with respect to the y-axis, x-axis and origin. You will also learn how to test for symmetry of a given function? A graph is symmetric with respect to the y-axis if, whenever (x, y) is a point on the graph, then (-x, y) is also a point on the graph. This means that the portion of the graph to the left of the axis is a mirror image of the portion to the right of the axis. A graph is symmetric with respect to the axis if, whenever (x, y) is a point on the graph, then (x, -y) is also a point on the graph. This means that the portion of the graph below the axis is a mirror image of the portion above the axis. A graph is symmetric with respect to the origin if, whenever (x, y) is a point on the graph, then (-x, -y) is also a point on the graph. This means that the graph is unchanged by a rotation of about the origin.
Tests for Symmetry.
The graph of an equation in and is symmetric with respect to the y-axis when replacing x by -x yields an equivalent equation.
The graph of an equation in and is symmetric with respect to the x-axis when replacing y by -y yields an equivalent equation.
The graph of an equation in and is symmetric with respect to the origin when replacing x by -x and y by -y yields an equivalent equation.
The graph of a polynomial has symmetry with respect to the y-axis when each term has an even exponent (or is a constant). Similarly, the graph of a polynomial has symmetry with respect to the origin when each term has an odd exponent.