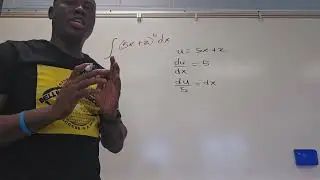Definite Integral #
Definition and Notation
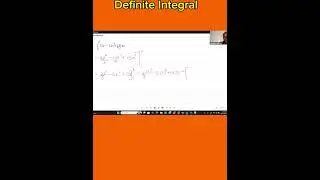
The definite integral
∫baf(x)dx∫abf(x)dx
is an integral to be evaluated between a lower limit aa and upper limit bb.
By the fundamentaltheorem of calculus, if F(x)F(x) is the antiderivative of f(x)f(x), then
∫baf(x)dx=F(b)−F(a).∫abf(x)dx=F(b)−F(a).
When computing a definite integral, it is conventional to use square brackets in the following way to denote that the antiderivative F(x)F(x) is to be evaluated between limits aa and bb.
∫baf(x)dx=[F(x)]ba=F(b)−F(a).