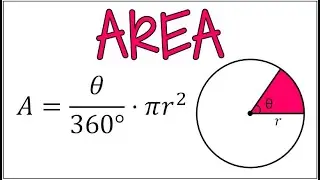
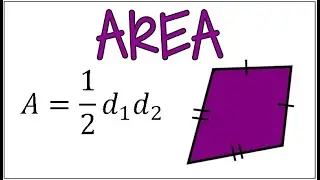
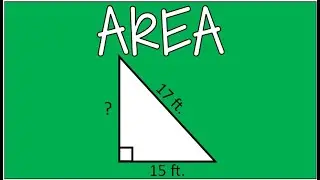
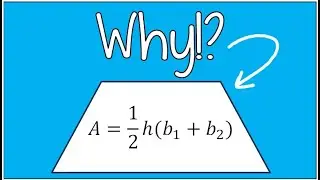Finding the Inverse of a Function After Applying Restricted Domain
Inverse Functions! A function has an inverse if it is one-to-one (Don't know what that means? Watch this: • One-to-One? How to Use a Horizontal L... ). In this example, we start with a restriction since the original function would not be one-to-one. After restricting the domain, our function us one-to-one and we can proceed with finding the inverse function. To find the inverse, first change the f(x) to a y. Then, switch your y and x variables and solve for y. Then, change your y to f^-1(x) (this means f inverse of x). It is also very helpful to graph your original function and the inverse function. This way you can check to see if you need to put any restrictions on your inverse (See an example like that here: • Finding the Inverse of a Square Root ... ).
Have a specific question or video idea? Email [email protected]
#midnightmathtutor #inversefunctions #inversefunction
Enjoying our videos? Give us a like, comment, and subscribe!
Font used in thumbnail/logo: KG Drops of Jupiter
