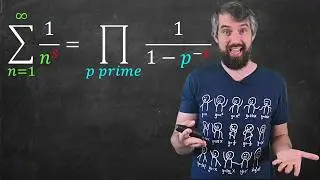Reflexive, Symmetric, and Transitive Relations on a Set

Опубликовано: 11 Октябрь 2024
на канале: Dr. Trefor Bazett

342,398

5.6k

A relation from a set A to itself can be though of as a directed graph. We look at three types of such relations: reflexive, symmetric, and transitive.

A relation is reflexive if every element relates to itself, that is has a little look from itself to itself.
A relation is symmetric if whenever x relates to y, then y relates to x. This looks like every path between x and y has a path back.
A relation is transitive if whenever xRy and yRz, then xRz (this shorthands is read "x relates to y" and so on). This looks like every two step path has a corresponding 1 step path.

►FULL DISCRETE MATH PLAYLIST:    • Discrete Math (Full Course: Sets, Log...

OTHER COURSE PLAYLISTS:
►CALCULUS I:    • Calculus I (Limits, Derivative, Integ...
► CALCULUS II:    • Calculus II (Integration Methods, Ser...
►MULTIVARIABLE CALCULUS (Calc III):    • Calculus III: Multivariable Calculus ...
►VECTOR CALCULUS (Calc IV):    • Calculus IV: Vector Calculus (Line In...
►DIFFERENTIAL EQUATIONS:    • How to solve ODEs with infinite serie...
►LINEAR ALGEBRA:    • Linear Algebra (Full Course)

OTHER PLAYLISTS:
► Learning Math Series
   • 5 Tips To Make Math Practice Problems...
►Cool Math Series:
   • Cool Math Series

BECOME A MEMBER:
►Join:    / @drtrefor

MATH BOOKS & MERCH I LOVE:
► My Amazon Affiliate Shop: https://www.amazon.com/shop/treforbazett

SOCIALS:
►Twitter (math based):   / treforbazett
►Instagram (photography based):   / treforphotography