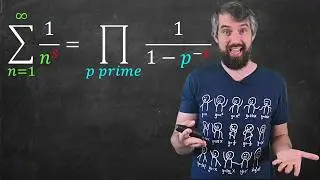Flow Integrals and Circulation // Big Idea, Formula & Examples // Vector Calculus
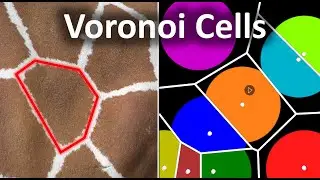
When a vector field is a velocity field, a natural phenomenon we can measure is the Flow. This accumulates the tendency of the vector field to be tangential to the curve. If we imagine our field is a velocity field, the flow is measuring the degree to which a curve just naturally flows along with that velocity field. As a line integral, this is identical to our formula for work, it is just interpreted differently physically. When the path is a closed curve - i.e. starts and ends at the same point - then the flow integral is called the circulation of the vector field along a path. We see as examples a source field which has no flow and a spin field which has lots of flow.
MY VECTOR CALCULUS PLAYLIST:
►VECTOR CALCULUS (Calc IV) • Calculus IV: Vector Calculus (Line In...
OTHER COURSE PLAYLISTS:
►DISCRETE MATH: • Discrete Math (Full Course: Sets, Log...
►LINEAR ALGEBRA: • Linear Algebra (Full Course)
►CALCULUS I: • Calculus I (Limits, Derivative, Integ...
► CALCULUS II: • Calculus II (Integration Methods, Ser...
►MULTIVARIABLE CALCULUS (Calc III): • Calculus III: Multivariable Calculus ...
►DIFFERENTIAL EQUATIONS: • How to solve ODEs with infinite serie...
OTHER PLAYLISTS:
► Learning Math Series
• 5 Tips To Make Math Practice Problems...
►Cool Math Series:
• Cool Math Series
BECOME A MEMBER:
►Join: / @drtrefor
MATH BOOKS & MERCH I LOVE:
► My Amazon Affiliate Shop: https://www.amazon.com/shop/treforbazett
SOCIALS:
►Twitter (math based): / treforbazett
►Instagram (photography based): / treforphotography