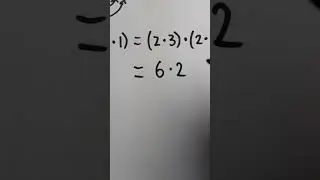Complement of Independent Set is Vertex Cover | Graph Theory
We prove the complement of an independent vertex set is a vertex cover. This makes for an easy direct proof once we recall our definitions. An independent vertex set is a set of vertices, no two of which are adjacent. A vertex cover is a set of vertices such that every edge has at least one end vertex in the cover. The vertex cover is said to cover the graph, or cover all edges of the graph. Then, if we take an arbitrary independent set X from a graph G, and take an edge uv from G, we know u is not in X or v is not in X. This is because if they were both in the independent set X - that would contradict X having no adjacent vertices. Thus, u is in X complement or v is in X complement. We see every edge has at least one end vertex in the complement of our independent set, and so the complement is a vertex cover. #GraphTheory
Independent Vertex Sets: • Independent Vertex Sets and Independe...
Vertex Covers: • Vertex Covers and Vertex Covering Num...
Complement of Vertex Cover is Independent Set: • Complement of Vertex Cover is Indepen...
Graph Theory playlist: • Graph Theory
★DONATE★
◆ Support Wrath of Math on Patreon for early access to new videos and other exclusive benefits: / wrathofmathlessons
◆ Donate on PayPal: https://www.paypal.me/wrathofmath
Thanks to Robert Rennie, Barbara Sharrock, and Rolf Waefler for their generous support on Patreon!
Thanks to Crayon Angel, my favorite musician in the world, who upon my request gave me permission to use his music in my math lessons: https://crayonangel.bandcamp.com/
Follow Wrath of Math on...
● Instagram: / wrathofmathedu
● Facebook: / wrathofmath
● Twitter: / wrathofmathedu
My Music Channel: / @emery3050