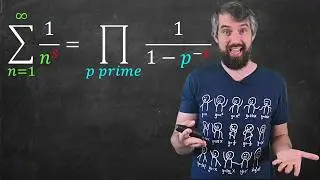Parseval's Identity, Fourier Series, and Solving this Classic Pi Formula
To celebrate #PiDay we solve the Basel Problem - that the sum of reciprocals of square naturals is pi^2/6 - using techniques from Fourier Analysis, in particular Parseval's Identity, which is a sort of infinite dimensional analog of Pythagoras.
Check out my intro playlist on FOURIER SERIES► • Intro to FOURIER SERIES: The Big Idea
Check out my MATH MERCH line in collaboration with Beautiful Equations
►https://beautifulequations.net/pages/...
0:00 The Basel Problem
1:06 Fourier Series Refresher
3:22 Parseval's Identity
5:13 Inner Products & Generalized Pythagoras
9:46 The proof that n^2/6=1/1+1/4+1/9...
COURSE PLAYLISTS:
►DISCRETE MATH: • Discrete Math (Full Course: Sets, Log...
►LINEAR ALGEBRA: • Linear Algebra (Full Course)
►CALCULUS I: • Calculus I (Limits, Derivative, Integ...
► CALCULUS II: • Calculus II (Integration Methods, Ser...
►MULTIVARIABLE CALCULUS (Calc III): • Calculus III: Multivariable Calculus ...
►VECTOR CALCULUS (Calc IV) • Calculus IV: Vector Calculus (Line In...
►DIFFERENTIAL EQUATIONS: • Ordinary Differential Equations (ODEs)
►LAPLACE TRANSFORM: • Laplace Transforms and Solving ODEs
►GAME THEORY: • Game Theory
OTHER PLAYLISTS:
► Learning Math Series
• 5 Tips To Make Math Practice Problems...
►Cool Math Series:
• Cool Math Series
BECOME A MEMBER:
►Join: / @drtrefor
SOCIALS:
►Twitter (math based): / treforbazett
►Instagram (photography based): / treforphotography