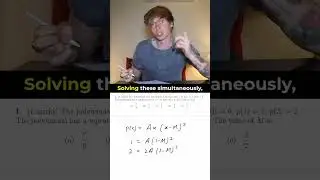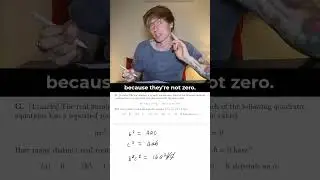Oxford Calculus: Finding Critical Points for Functions of Two Variables
University of Oxford Mathematician Dr Tom Crawford explains how to calculate the critical points for a function of two variables.
Just as the critical points for a function of one variable are found by differentiation, the same techniques can be applied to a multivariable function to determine where it is stationary.
We begin with a reminder of critical points for a function of one variable, before looking at partial differentiation of a multivariable function with a worked example.
Part 2 on classifying the critical points: • Oxford Calculus: Classifying 2D Criti...
The 3D plots used in the video are all generated by the Maple Calculator App which you can download for free from Google Play and the App Store.
Android: https://play.google.com/store/apps/de...
Apple: https://apps.apple.com/us/app/maple-c...
Find out more on the Maplesoft YouTube channel: / @maplesoft
Produced by Dr Tom Crawford at the University of Oxford.
Tom is an Early-Career Teaching and Outreach Fellow at St Edmund Hall: https://www.seh.ox.ac.uk/people/tom-c...
For more maths content check out Tom's website https://tomrocksmaths.com/
You can also follow Tom on Facebook, Twitter and Instagram @tomrocksmaths.
/ tomrocksmaths
/ tomrocksmaths
/ tomrocksmaths
Get your Tom Rocks Maths merchandise here:
https://beautifulequations.net/collec...